Despite its shortcomings, the Saint-Venant-Exner system remains the most widely used model for simulating sediment transport. However, simulation software that employs this model often encounters stability issues when there is strong interaction between the solid and liquid phases. How can these stability problems be addressed?
While numerous methods and techniques have been proposed to address this issue, they still fail to fully account for all aspects of stability. We propose articles offering more stable simulation methods for solving the model: a fully coupled scheme and a semi-coupled scheme.
This study focuses on to the numerical approximation of solutions for the 1D nonlinear shallow water model coupled with a sedimentary continuity equation described by the Saint-Venant-Exner system. This system comprises three equations: the two equations of the shallow water flow model, which include source terms for topography and friction, and a simple conservation law that accounts for the interaction between the fluid and the topography. \[\label{1}
\left\{
\begin{array}{lll}
\partial_{t}h +\partial_{x}(hu) =0,\qquad x\in \mathbb{R},\quad t>0 \\
\ \\
\partial_{t}hu +\partial_{x}\big( hu^{2}+g\dfrac{h^{2}}{2}\big)=-gh(\partial_{x}b+T_{f})\\
\ \\
(1-\phi)\partial_{t}b+\partial_{x}q_{s} =0
\end{array}
\right.\] The unknowns of the problem are the water height \(h(t, x)\geq0\), the flow velocity \(u(t, x)\) and \(b(x)\), which defines the bottom topography. The parameters include the gravitational acceleration \(g>0\) and the porosity of the sedimentary layer \(\phi\), which will later be set to zero. We also introduce the fluid discharge \(q(t, x) := h(t, x) u(t, x)\). The friction term \(T_{f}\) and the sediment flux \(q_{s}\) are fundamental elements of the model, because they ensure the coupling between the fluid and the solid parts.
\[\begin{aligned} \label{3} & W=\begin{pmatrix} h\\ q\\ b \end{pmatrix},\quad f(W) =\begin{pmatrix} q\\ \dfrac{q^{2}}{h}+\dfrac{gh^{2}}{2}\\ q_{s} \end{pmatrix},\quad S(W)=\begin{pmatrix} 0\\ -gh\big(\partial_{x}b-T_{f}\big)\\ 0 \end{pmatrix}.\nonumber \end{aligned}\] We introduce the Jacobian matrix of the problem, \[\label{r14} A= \begin{bmatrix} 0 &1 &0 \\ gh-u^{2} &2u & gh \\ \alpha & \beta & 0 \end{bmatrix} \quad \text{avec} \quad \alpha=\dfrac{\partial q_{s}}{\partial h}, \quad \beta=\dfrac{\partial q_{s}}{\partial q} \quad \text{et} \quad q=hu .\] Thus the vector formulation of [1] is defined by \[\label{5} \partial_{t}(W)^{T} +A(W)\partial_{x}W= S(W),\]
For a given initial condition, At time \(t^{n+1}\) the updated state \(W^{n+1}_{i}\) is given by \[\begin{aligned} \label{14} W^{n+1}_{i}=W^{n}_{i}-\dfrac{\Delta t}{\Delta x}\big(F(W_{i}^{n},W_{i+1}^{n})-F(W_{i-1}^{n},W_{i}^{n})\big)\nonumber\\ +\dfrac{\Delta t}{2}(\bar{S}_{;1/2}-\bar{S}_{;-1/2}),\end{aligned}\] with \[\bar{S}_{;1/2}=\bar{S}(W_{i}^{n},W_{i+1}^{n}),\] \(\bar{S}\) must be defined according to a consistent discretization of \(S\) and \(F\) is the numerical flux that we constructed to obtain a stable, consistent scheme capturing all stationary states.
\[\label{15} F( W_{L},W_{R})=\dfrac{1}{2}\big(f(W_{R}) + f(W_{L})\big)-\dfrac{\Delta x}{4\Delta t}( W_{R}- W_{L})+\dfrac{\Delta x}{2\Delta t}(J^{+}_{LR}-J^{-}_{LR}),\] where \[\label{16a} J^{-}_{LR}=\dfrac{1}{\Delta x}\int_{-\Delta x/2}^{0}\tilde{W}_{\mathcal{R}}(\dfrac{x}{\Delta t} W_{L},W_{R})dx\] \[\label{16b} J^{+}_{LR}=\dfrac{1}{\Delta x}\int_{0}^{\Delta x/2}\tilde{W}_{\mathcal{R}}(\dfrac{x}{\Delta t} W_{L},W_{R})dx,\] Where \(\tilde{W}_{\mathcal{R}}(x/t; w_{L},w_{R},b_{L},b_{R})\) is the approximate Riemann solver.
To illustrate the behavior of the proposed scheme, which we will refer to as the Fully Well-Balanced Corrected Scheme with Nickalls (FWBCN), here, we present numerical simulation results of dune evolution in river flow and dam break on dry bottom topography. For the first test cases, we compare our results with those obtained by the well-known SimSol scheme, which has already been judged superior to three other methods.
The first case is a sediment transport problem that considers a hump under the flow of a river. The channel length is \(L = 1000 \, \text{m}\). \[\label{2}
\begin{cases}
b(0,x)=\begin{cases}
0.1+\sin^{2}\big( \dfrac{(x-300)\pi}{200}\big), \quad \text{si}\quad 300\leqslant x\leqslant 500,\\
0.1\quad \text{ sinon},
\end{cases}\\
h(0,x)=10-b(0,x),\\
u(0,x)=\dfrac{q_{0}}{h(0,x)},\quad q_{0}=10m^{2}/s.
\end{cases}\] With a discretization of 2000 cells for domain, the figure 1 show us the the bottom topography at time \(t = 750 s\). It appears that the scheme presented is the most accurate.

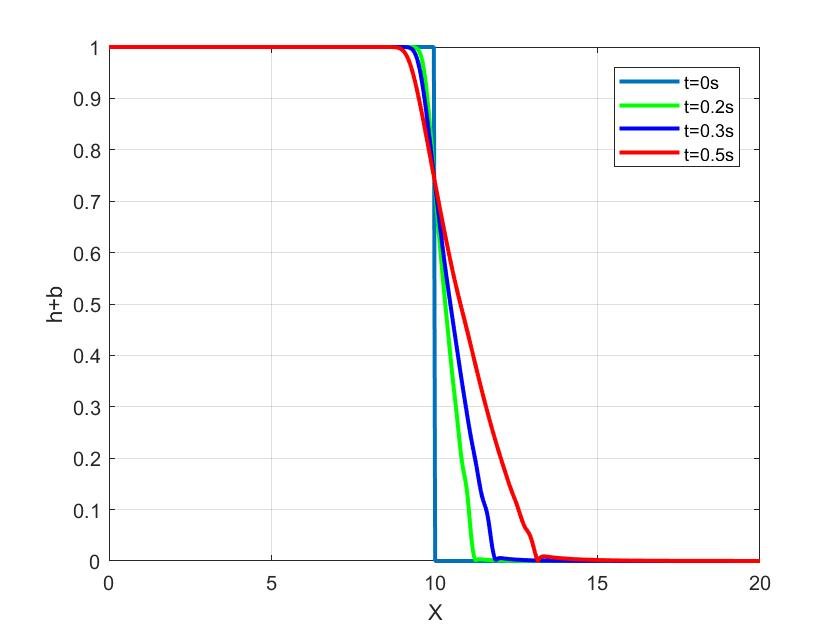
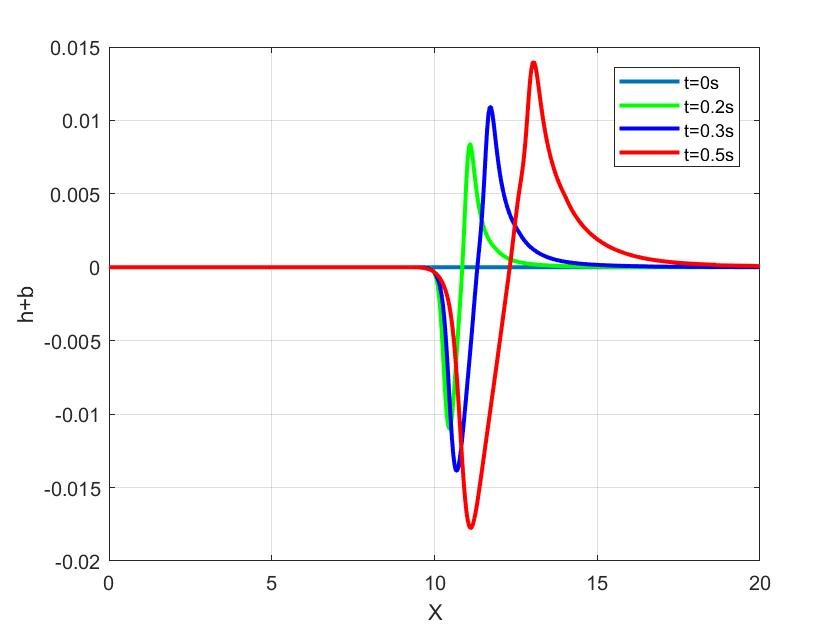
For second test case, we consider a dam break on a flat and dry bottom. The domain is \([0, 10]\) with a flat topography. The initial data are defined by, \[h(0,x)=\begin{cases} 2m, \quad \text{if}\quad x\leqslant 10,\\ 0m, \quad \text{if}\quad x> 10, \end{cases}\] The domain is discretized into 500 cells, and the approximate solutions at different times are displayed in Figure 3.. As with the previous test case, the FWCN scheme manges to solve the physical phenomenon since there is no instability.
Here, at date \(t^{n}\), we assume that an approximation of the bathymetry is known, \[b(x,t^{n})=\{b^{n}_{i}\}_{i=1}^{nx} \quad \text{pour}\quad x \in [0,L],\] and we now look for its evolution \(\{b^{n+1}_{i}\}_{i=1}^{nx}\) at time \(t^{n+1} = t ^{n} + \Delta t\). To do this we will have to solve the following problem: \[\label{5AA} (1-\phi)\partial_{t}b\big(x,t^{n}\big)+\partial_{x}q_{s}\big(h^{n+1},u^{n+1}\big) =0,\] where \(\big(h^{n+1},u^{n+1}\big)\) satisfies the Saint-Venant equations: \[\label{1M} \left\{ \begin{array}{lll} \partial_{t}h +\partial_{x}(hu) =0,\qquad x\in \mathbb{R},\quad t>0 \\ \ \\ \partial_{t}hu +\partial_{x}\big( hu^{2}+g\dfrac{h^{2}}{2}\big)=-gh(\partial_{x}b+T_{f}) \end{array} \right.\]
Approach
Our approach is to:
design a Godunov-type scheme capturing all steady states for the shallow water model for the resolution of [1M],
a finite difference approximation well suited to the resolution of [5AA],
ensure the coupling between the hydraulic and morphodynamic parts.
Successful management of the coupling between solid and liquid parts
instead of using the wave speeds given by the Saint-Venant model [1M] defined by: \[\label{r17a}
\lambda_{L}= u- \sqrt{gh},\qquad \lambda_{R}= u+ \sqrt{gh},\] we use those given by the coupled Saint-Venant-Exner model [1] considering that there is no sediment transport therefore \(\beta =0\) to obtain: \[\label{r17b}
\lambda_{L}=\dfrac{2}{3}\bigg( u- \sqrt{u^{2}+3gh}\bigg)< 0,\quad \lambda_{R}=\dfrac{2}{3}\big( u+ \sqrt{u^{2}+3gh}\big)> 0.\]
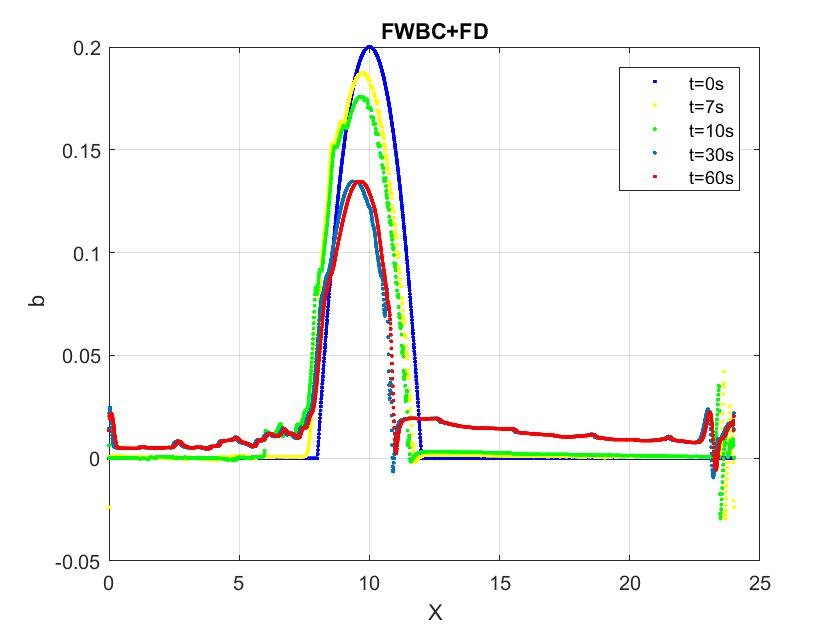
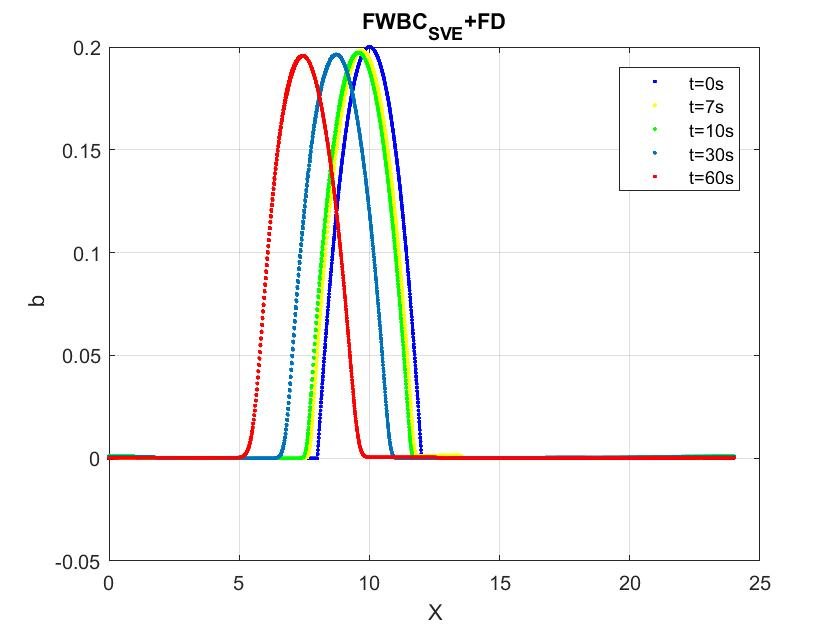
Simulation
As an illustration, we study the simulation of dune evolution in torrential flow regimes and compare the results obtained by two different numerical strategies:
\[b(0,x)=\begin{cases} 0.2 -0.05(x - 10)^{2}, \hspace{1.5cm}\text{ if } 8 \leq x\leq 12 m \\ 0 \hspace{5cm}\text{otherwise}. \end{cases}\]
Simulation result