Nowadays, surface water is used a lot in human activities. Hydraulic structures are often built to ensure optimal use of this water. This is the example of irrigation canals and navigable rivers. Our contribution is to ensure the stability of the water in these structures by feedback controls placed at the ends of the structures. In the literature this stability has already been obtained when the channel is rectangular. In our case we manage to obtain stability when the channel is trapezoidal, which is more practical and economical.
The most general version of \(1D\) Saint-Venant equations with arbitrary varying slope, section profile and friction model is given by the following system (see Adhémar Barré, 1871):
\[\label{a1}
\left\{
\begin{array}{lll}
\partial_{t} A
+\partial_{x}(AV) =0,\\
\ \\
\partial_{t}(AV)+\partial_{x}(V^{2}A )+gA\partial_{x}H= gA \big(S_{0}-S_{f}(A,V,x)\big),\\
\end{array}
\right.\]
where A is the cross-sectional area of the section, V is the velocity, \(\textbf{H}(A, x)\) is the water depth, g is the gravity acceleration, \(\textbf{S}_{0}\) is the channel slope, \(\textbf{S}_{f}\) is the friction slope, it is usually defined by semi-empirical formulae proposed by hydraulic engineers in the late nineteenth or early twentieth centuries. In general, it only depends on the fluid quantities. One of the most popular is \(S_{f}=k\dfrac{V^{2}}{A}\), where k is a constant friction coefficient.
For a trapezoidal section, the system [a1] can now be written as \[\label{1}
\left\{
\begin{array}{lll}
\partial_{t}A +\partial_{x}AV=0,\\
\ \\
\partial_{t}V+V\partial_{x}V+\dfrac{g}{\sqrt{b^{2}+4mA}}\partial_{x}A=g (S_{0}-S_{f}),\\
\end{array}
\right.\] where \(b = b(x)\) is the channel width at the bottom and \(m = m(x)\) is the inverse slope of the channel walls.
Steady-state
A steady-state of the system [a1] is a constant state \(( A^{*} , V^{*})\) which satisfies the relation \[\label{a2}
\left\{
\begin{array}{lll}
A^{*}V^{*}=Q^{*}\quad \text{or}\quad A^{*}\partial_{x}V^{*}+V^{*}\partial_{x}A^{*}=0,\\
\ \\
V^{*}\partial_{x}V^{*}+\dfrac{g}{\sqrt{b^{2}+4mA^{*}}}\partial_{x}A^{*}= g (S_{0}-k\dfrac{V^{*2}}{A^{*}}),\\
\end{array}
\right.\]
Goal
Our goal is to ensure the exponential stability of the steady states of the nonlinear system [a1] under some boundary conditions of the form: \[\label{a5}
V(t, 0) = \mathcal{K}\big(A(t, 0)\big),\quad V(t, L) = \mathcal{K}\big(A(t, L)\big),\]
where \(\mathcal{K}:\mathbb{R}\rightarrow\mathbb{R}\) is of class \(C^{2}\).
For any given initial condition \[\label{a7}
A(0,x)=A_{0},\quad V(0,x)=V_{0},\quad
x\in[0,L],\] such that the well-posedness of the system [a1], [a5] and [a7] is guarantee for sufficiently small initial data (see Bastin & Coron, 2016, Appendix A).
We have the following result:
The nonlinear Saint-Venant system [a1]-[a5]-[a7] is exponentially stable for the \(H^{2}\)-norm provided that the boundary conditions satisfy \[\begin{aligned}
&\mathcal{K}'(A^{*}(0))\in \bigg(\dfrac{-g}{V^{*}(0)\sqrt{b^{2}+4mA^{*}(0)}},-\dfrac{V^{*}(0)}{A^{*}(0)}\bigg),\label{9a} \\
& \text{and}\nonumber\\ &\mathcal{K}'(A^{*}(L)) \in\mathbb{R}\diagdown \bigg(\dfrac{-g}{V^{*}(L)\sqrt{b^{2}+4mA^{*}(L)}},-\dfrac{V^{*}(L)}{A^{*}(L)}\bigg).\label{9b}
\end{aligned}\]
For the proof of the theorem 1, we first prove the exponential stability result for the linearized system for the \(L^{2}\)-norm by finding a suitable Lyapunov function. Then we show that this Lyapunov function enables us to obtain the exponential stability for the \(H^{2}\)-norm for the nonlinear system under boundary control conditions [a5] with properties [9a]-[9b].
Exponential stability of the linearized system
We define the perturbation functions a and v as \[\label{pt}
a(t,x) =A(t,x)-A^{*}(x), \quad \text{and}\quad v(t,x) =V(t,x)-V^{*}(x).\] The linearization of the system [a1] about the steady-state is \[\label{a3}
\begin{pmatrix}
a\\
v
\end{pmatrix}_{t} +\begin{pmatrix}
V^{*}& A^{*} \\
\dfrac{g}{\sqrt{b^{2}+4mA^{*}}}&V^{*}
\end{pmatrix}\begin{pmatrix}
a\\
v
\end{pmatrix}_{x}+\begin{pmatrix}
V_{x}^{*}&\quad A^{*}_{x} \\
f^{*}_{w} &\quad V^{*}_{x}+2gk\dfrac{V^{*}}{A^{*}}
\end{pmatrix}\begin{pmatrix}
a\\
v
\end{pmatrix}=0\]
where \(f^{*}_{w}\) is defined by \[\label{15}
f^{*}_{w}=gk\dfrac{V^{*2}}{A^{*2}}+\dfrac{2mgA^{*}V^{*2} (S_{0}-k\dfrac{V^{*2}}{A^{*}})}{\big(V^{*2}\sqrt{b^{2}+4mA^{*}}-gA^{*}\big)\big(b^{2}+4mA^{*}\big)},\]
The corresponding linearization of the boundary conditions [a5] is given by \[\label{a10}
v(t,0)=k_{0}a(t,0),\quad v(t,L)=k_{1}a(t,L),\] where \[%\label{a11}
k_{0}=\mathcal{K}'(A^{*}(0)),\quad k_{1}=\mathcal{K}'\big(A^{*}(L)\big).\]
With an initial condition given as follows \[\label{a12}
a(0,x)=a_{0}(x),\quad v(0,x)=v_{0}(x),\] where \((a_{0}, v_{0})^{T} \in L^{2}((0, L); \mathbb{R}^{2})\),
the Cauchy problem [a3], [a10] and [a12] is well-posed (see Bastin & Coron, 2016, Appendix B) and now, the exponential stability of the linearized system is a problem of null-stabilization for a and v.
We have the following result:
For the linearized Saint-Venant system [a3], [a10] and [a12], if the boundary conditions satisfy \[\begin{aligned}
&k_{1}\in\bigg(\dfrac{-g}{V^{*}(0)\sqrt{b^{2}+4mA^{*}(0)}},-\dfrac{V^{*}(0)}{A^{*}(0)}\bigg),\\
& \text{and}\nonumber\\
& k_{2} \in \mathbb{R}\diagdown \bigg(\dfrac{-g}{V^{*}(L)\sqrt{b^{2}+4mA^{*}(L)}},-\dfrac{V^{*}(L)}{A^{*}(L)}\bigg)\end{aligned}\] Then there exist a constant \(\alpha > 0\) and \(g_{1},g_{2}\in C^{1}\big([0,L]\rightarrow(0,+\infty)\big)\) such that the following control Lyapunov function candidate \[\begin{aligned}
\label{lf2}
V(a,v)=&\int_{0}^{L}\big(g_{1}+g_{2}\big) \bigg(\dfrac{g}{A^{*}\sqrt{b^{2}+4mA^{*}}}h^{2}\nonumber\\
&+2\dfrac{g_{1}-g_{2}}{g_{1}+g_{2}}\sqrt{\dfrac{g}{A^{*}\sqrt{b^{2}+4mA^{*}}}}vh +v^{2}\bigg)dx\end{aligned}\] verifies: \[\label{cc2}
\dfrac{d}{dt}(V(a(t,\cdot),v(t,\cdot)))\leq -\alpha V(a(t,\cdot),v(t,\cdot)),\] for any \((a, v) \in L^{2}\big((0, L),\mathbb{R}^{2}\big)\) solution of the system [a3], [a10] and [a12]. In the distribution sense which implies the exponential stability of the linearized system [a3], [a10] and [a12] for the \(L^{2}\)-norm.
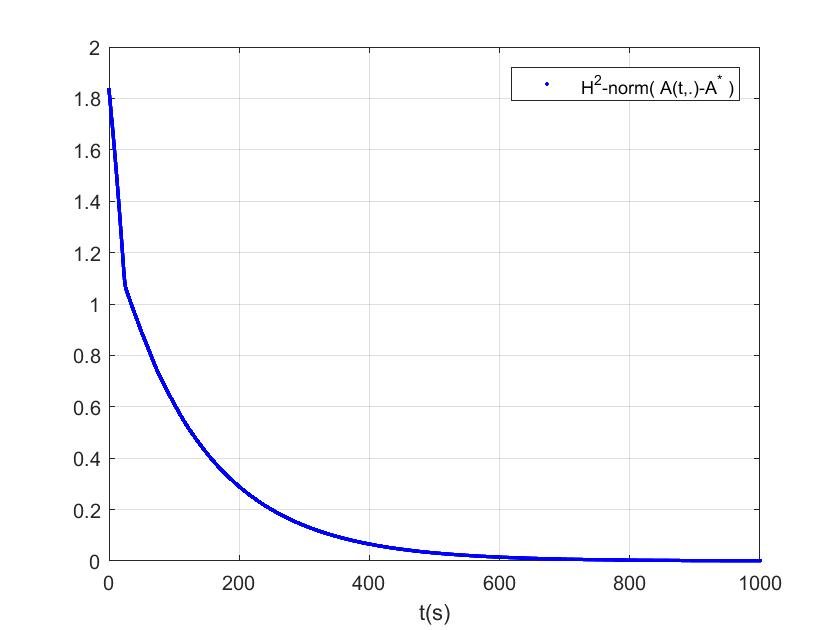
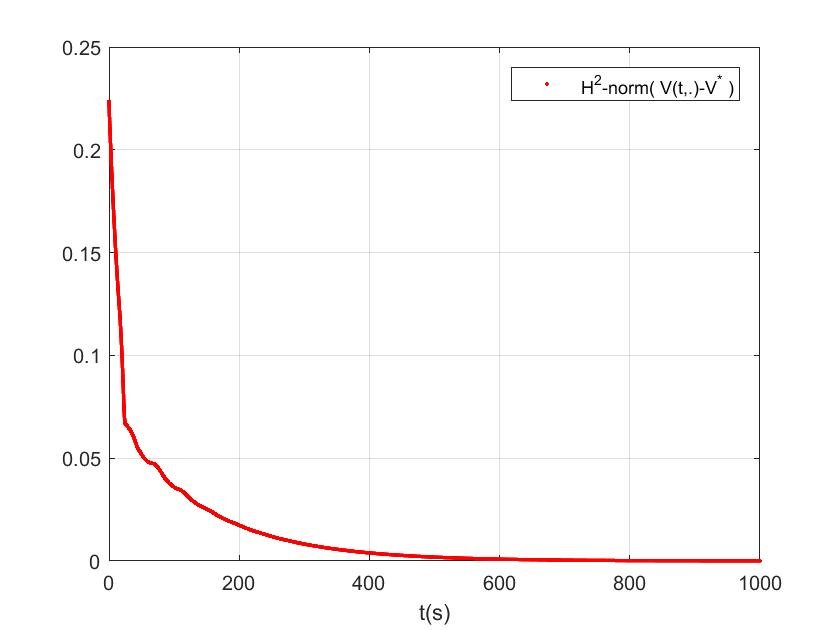
Numerical simulation
Illustration du théorème en fournissant des simulations numériques de la \(H^{2}\)-norme des solutions du système non linéaire [1], [a3] et [a7].
: \[L = 1000m ,\quad b(x) =1,\quad \text{et}\quad m(x) =1+5x/L,\]
: \[\begin{aligned}
&A^{*}(0)= 6m^{2},V^{*}(0)= 0.5m/s,\nonumber\\
& a(0,x)= 0.6m^{2}, v(0,x)= 0.05m/s\\
&S_{b} = 2kV^{*2}(0)/A^{*}(0),\quad k = 0.002\nonumber
\end{aligned}\]
: \[\begin{aligned}
&\mathcal{K}'\big(A(t, 0)\big)= -1.1V^{*}(0)/A^{*}(0),\\
&\mathcal{K}'\big(A(t, L)\big)= -0.9V^{*}(L)/A^{*}(L)
\end{aligned}\]
Simulation result